How To Find Direction Angle

In physics, sometimes you lot have to discover the angle and magnitude of a vector rather than the components. To notice the magnitude, you lot use the Pythagorean theorem. And to find

you use the changed tangent office (or inverse sine or cosine).

For example, assume you're looking for a hotel that'south 20 miles e so 20 miles due north. From your present location, what is the angle (measured from east) of the management to the hotel, and how far away is the hotel? Y'all can write this problem in vector notation, like so:

Step i: (20, 0)

Step two: (0, 20)

When calculation these vectors together, you get this result:

(20, 0) + (0, 20) = (20, 20)

The resultant vector is (20, xx). That'south one way of specifying a vector — employ its components. But this trouble isn't request for the results in terms of components. The question wants to know the angle and altitude to the hotel.

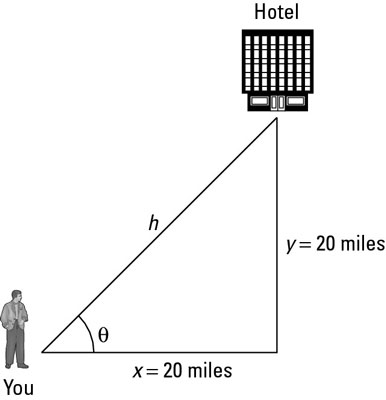
Using the angle created by a vector to get to a hotel.

In other words, looking at the above figure, the problem asks,

If yous know a vector's vertical and horizontal components, finding the vector'due south magnitude isn't then hard because you just need to detect the hypotenuse of a right triangle. You tin use the Pythagorean theorem (ten ⁱⁱ + y ² = h ²), solved for h:

Plugging in the numbers gives you

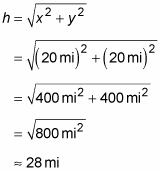
Continue in mind that when y'all know the horizontal and vertical components of a vector, y'all can use the tangent to detect the angle considering

All you have to do is take the changed tangent of y/x:

Suppose you drive 20 miles east and xx miles north. Here's how y'all detect

the angle between your original position and your final 1:

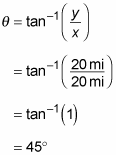
So the hotel is about 28 miles abroad at an angle of 45 degrees.

Be careful when doing calculations with inverse tangents, because angles that differ by 180 degrees have the same tangent. When you have the inverse tangent, you lot may need to add or subtract 180 degrees to go the actual angle you desire. The inverse tangent push button on your calculator volition e'er give you lot an bending between 90 degrees and –90 degrees. If your angle is non in this range, so yous accept to add together or subtract 180 degrees.

For this example, the answer of 45 degrees must be correct. But consider a state of affairs in which you lot'd need to add or subtract 180 degrees: Suppose that you walk in completely the opposite direction to the hotel. You walk twenty miles west and xx miles south (ten = –20 miles, y = –20 miles), so if you use the aforementioned method to work out the angle, you get the post-obit:

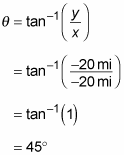
Yous get the same answer for the angle even though you're walking in completely the opposite direction equally before! That's because the tangents of angles that differ by 180 degrees are equal. Simply if y'all look at the components of the vector (x = –20 miles, y = –20 miles), they're both negative, and then the bending must be between -90 degrees and -180 degrees. If you decrease 180 degrees from your answer of 45 degrees, you go –135 degrees, which is your actual angle measured from the positive x-axis in the clockwise direction.

Alternatively, y'all could reason that since the components of the vector are both negative, you lot must be betwixt 180 degrees and 270 degrees. You would and then add 180 degrees to your outcome and get 225 degrees, which would be measured from the positive x-axis in the counterclockwise direction.

So, which bending is correct, 225 degrees or -135 degrees? Both! Whether you move counterclockwise 225 degrees or clockwise 135 degrees from the positive x-axis, y'all end upwards heading the same direction.

How To Find Direction Angle,

Source: https://www.dummies.com/article/academics-the-arts/science/physics/how-to-find-the-angle-and-magnitude-of-a-vector-173966/

Posted by: washingtontured1978.blogspot.com

Share this post